먼저 데이터를 불러온 후 null 값을 처리하고 시각화 해보았습니다.
(데이터: https://www.kaggle.com/c/rossmann-store-sales)
import pandas as pd
import numpy as np
store = pd.read_csv("../rossmann-store-sales/store.csv")
train = pd.read_csv("../rossmann-store-sales/train.csv")
test = pd.read_csv("../rossmann-store-sales/test.csv")
store.isnull().sum()
store.fillna(0, inplace=True)
train.isnull().sum()
test.fillna(0, inplace=True)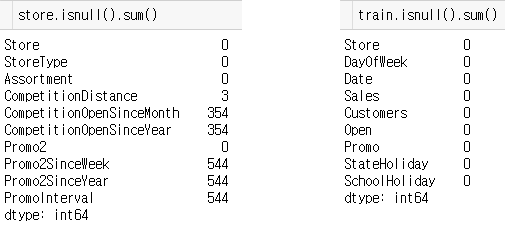
import seaborn as sns
sns.countplot(x = 'DayOfWeek', hue = 'Open', data = train)
plt.title('Store Daily Open Countplot')
sns.countplot(x = 'DayOfWeek', hue = 'Open', data = test)
plt.title('Store Daily Open Countplot')
Data Pre-processing
# store 데이터 merge
train = pd.merge(train, store, on='Store')
test = pd.merge(test, store, on='Store')
train = train.sort_values(['Date'],ascending = False)
train_total = train.copy()
split_index = 6*7*1115
valid = train[:split_index]
train = train[split_index:]
# only use data of Sales>0 and Open is 1
valid = valid[(valid.Open != 0)&(valid.Sales >0)]
train = train[(train.Open != 0)&(train.Sales >0)]
train_total = train_total[(train_total.Open != 0)&(train_total.Sales >0)]
train['Date'] = pd.to_datetime(train['Date'])
valid['Date'] = pd.to_datetime(valid['Date'])
train_total['Date'] = pd.to_datetime(train_total['Date'])
test['Date'] = pd.to_datetime(test['Date'])# process train and test
def process(data, isTest = False):
# label encode some features
mappings = {'0':0, 'a':1, 'b':2, 'c':3, 'd':4}
data.StoreType.replace(mappings, inplace=True)
data.Assortment.replace(mappings, inplace=True)
data.StateHoliday.replace(mappings, inplace=True)
# extract some features from date column
data['Month'] = data.Date.dt.month
data['Year'] = data.Date.dt.year
data['Day'] = data.Date.dt.day
data['WeekOfYear'] = data.Date.dt.weekofyear
# calculate competiter open time in months
data['CompetitionOpen'] = 12 * (data.Year - data.CompetitionOpenSinceYear) + \
(data.Month - data.CompetitionOpenSinceMonth)
data['CompetitionOpen'] = data['CompetitionOpen'].apply(lambda x: x if x > 0 else 0)
# calculate promo2 open time in months
data['PromoOpen'] = 12 * (data.Year - data.Promo2SinceYear) + \
(data.WeekOfYear - data.Promo2SinceWeek) / 4.0
data['PromoOpen'] = data['PromoOpen'].apply(lambda x: x if x > 0 else 0)
# Indicate whether the month is in promo interval
month2str = {1:'Jan', 2:'Feb', 3:'Mar', 4:'Apr', 5:'May', 6:'Jun', \
7:'Jul', 8:'Aug', 9:'Sept', 10:'Oct', 11:'Nov', 12:'Dec'}
data['month_str'] = data.Month.map(month2str)
def check(row):
if isinstance(row['PromoInterval'],str) and row['month_str'] in row['PromoInterval']:
return 1
else:
return 0
data['IsPromoMonth'] = data.apply(lambda row: check(row),axis=1)
# select the features we need
features = ['Store', 'DayOfWeek', 'Promo', 'StateHoliday', 'SchoolHoliday',
'StoreType', 'Assortment', 'CompetitionDistance',
'CompetitionOpenSinceMonth', 'CompetitionOpenSinceYear', 'Promo2',
'Promo2SinceWeek', 'Promo2SinceYear', 'Year', 'Month', 'Day',
'WeekOfYear', 'CompetitionOpen', 'PromoOpen', 'IsPromoMonth']
if not isTest:
features.append('Sales')
data = data[features]
return data
train = process(train)
valid = process(valid)
train_total = process(train_total)
x_test = process(test,isTest = True)# sort by index
valid.sort_index(inplace = True)
train.sort_index(inplace = True)
train_total.sort_index(inplace = True)
# split x and y
x_train, y_train = train.drop(columns = ['Sales']), np.log1p(train['Sales'])
x_valid, y_valid = valid.drop(columns = ['Sales']), np.log1p(valid['Sales'])
x_train_total, y_train_total = train_total.drop(columns = ['Sales']), np.log1p(train_total['Sales'])xgboost:
import xgboost as xgb
params = {"objective": "reg:linear", # for linear regression
"booster" : "gbtree", # use tree based models
"eta": 0.03, # learning rate
"max_depth": 10, # maximum depth of a tree
"subsample": 0.9, # Subsample ratio of the training instances
"colsample_bytree": 0.7, # Subsample ratio of columns when constructing each tree
"silent": 1, # silent mode
"seed": 10 # Random number seed
}
num_boost_round = 4000
dtrain = xgb.DMatrix(x_train, y_train)
dvalid = xgb.DMatrix(x_valid, y_valid)
watchlist = [(dtrain, 'train'), (dvalid, 'eval')]
# train the xgboost model
model = xgb.train(params, dtrain, num_boost_round, evals=watchlist, \
early_stopping_rounds= 100, feval=rmspe_xg, verbose_eval=True)Random Forest:
from sklearn.ensemble import RandomForestRegressor
clf = RandomForestRegressor(n_estimators = 15)
clf.fit(x_train, y_train)
# validation
y_predRF = clf.predict(x_valid)Decision Tree:
# Decision Tree Regressor
from sklearn.tree import DecisionTreeRegressor
dt = DecisionTreeRegressor(random_state=0)
dt.fit(x_train, y_train)
# validation
y_predDT = dt.predict(x_valid)Stacked (Ensemble):
# Stacked pred
stacked_pred = np.array([y_predRF, y_predDT, y_pred])
stacked_pred = np.transpose(stacked_pred)
from sklearn.linear_model import LinearRegression
lr_final = LinearRegression()
lr_final.fit(stacked_pred, y_valid)
final_pred = lr_final.predict(stacked_pred)rmseXGB = mean_squared_error(np.expm1(y_valid), np.expm1(y_pred), squared=False)
rmseRF = mean_squared_error(np.expm1(y_valid), np.expm1(y_predRF), squared=False)
rmseDT = mean_squared_error(np.expm1(y_valid), np.expm1(y_predDT), squared=False)
stacked_RMSE = mean_squared_error(np.expm1(y_valid), np.expm1(final_pred), squared=False)
print('XGB: {}\nRF: {}\nDT: {}\nStacked: {}'.format(rmseXGB, rmseRF, rmseDT, stacked_RMSE))

결과값은 Decision Tree, Random Forest, XGBoost, Ensemble 순서로 점차 좋아지는 것을 확인 할 수 있었습니다.
결과값들을 확인 후, 각각의 모델들을 이용해 아래 수식과 같은 Bayesian regression 모델을 만들어 보았습니다.
pymc3 라는 베이지안 회귀를 쉽게 해줄 수 있는 좋은 library 를 사용하였습니다.

import pymc3 as pm
with pm.Model() as linear_model:
# Intercept
intercept = pm.Normal('Intercept', mu = 0, sd = 10)
# Slope
slope = pm.Normal('slope', mu = 0, sd = 10)
slope2 = pm.Normal('slope2', mu = 0, sd = 10)
slope3 = pm.Normal('slope3', mu = 0, sd = 10)
# Standard deviation
sigma = pm.HalfNormal('sigma', sd = 10)
# Estimate of mean
mean = intercept + slope * Xtrain['XGB'][:500] + slope2 * Xtrain['RF'][:500]
+ slope3 * Xtrain['DT'][:500]
# Observed values
Y_obs = pm.Normal('Y_obs', mu = mean, sd = sigma, observed = y_valid[:500])
# Sampler
step = pm.NUTS()
# Posterior distribution
linear_trace = pm.sample(1000, step)pm.traceplot(linear_trace, figsize = (12, 12));
pm.plot_posterior(linear_trace, figsize = (12, 10));
Bayesian Regression 을 이용한 결과는 위 그래프와 같았습니다. 결과를 비교해 보기위해 평균값을 이용하여 수식을 세운 후 실제 값과 mean squared error 을 측정해 보았습니다.
eq = -0.43 + 0.92 * Xtrain.XGB[:500] + 0.25 * Xtrain.RF[:500] - 0.12 * Xtrain.DT[:500]
bayesian = mean_squared_error(np.expm1(y_valid[:500]), np.expm1(eq[:500]), squared=False)
ensemble = mean_squared_error(np.expm1(y_valid[:500]), np.expm1(final_pred[:500]), squared=False)
print('bayesian: %.2f\nensemble: %.2f'%(bayesian, ensemble))
from sklearn.metrics import mean_absolute_error
bayesian = mean_absolute_error((y_valid[:500]), (eq[:500]))
ensemble = mean_absolute_error((y_valid[:500]), (final_pred[:500]))
print('bayesian: %.2f\nensemble: %.2f'%(bayesian, ensemble))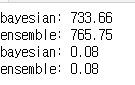
fig, ax1 = plt.subplots(figsize = (18,12))
ax2 = ax1.twinx()
x = np.arange(0, 500, 1)
y = np.expm1(y_valid[:500])
yhat = np.expm1(eq[:500])
ax1.plot(x, y, 'r-')
ax2.plot(x, yhat, 'g-')
ax1.set_xlabel('X data')
ax1.set_ylabel('Y1 data', color='r')
ax2.set_ylabel('Y2 data', color='g')
plt.show()
위와 같이 이번 포스트에서는 시계열 데이터를 이용하여 회귀 계수에 대한 분포를 제공하였습니다. 논문의 목적과는 조금 다르게 VaR을 계산 하지는 않았지만 예측하는데 있어서 높은 정확도의 분포를 얻을 수 있었습니다. 이러한 분포에 도메인지식을 고려하여 몇가지 모델들을 ensemble 해준다면 유의미한 시계열 예측 및 분석이 가능할 것으로 보입니다.
1. (사물·장소 등을) find, look (for), search (for), hunt (for), (formal) seek; (위치를) locate; (되찾다) recover
2. (사람을) find, look (for), search (for), hunt (for); (호출하다) want, ask for
3. (방문하다) visit, call (in/on), look sb up, (informal) drop by, (informal) drop in (on)
반응형
'3. 심화 학습 (Advanced Topics) > 연구실' 카테고리의 다른 글
| 간단한 BERT 모델을 이용하여 GPT 챗봇 성능 높이기 (1) | 2023.11.23 |
|---|---|
| [논문분석] 딥러닝을 이용하여 불규칙적인 시계열 예측 모델 만들기 (LSTNet) (0) | 2023.01.17 |
| 시계열 분석에서 예측 모델의 구축 및 Stacking을 위한 베이지안 회귀 분석 방법 (1/2) - 설명 (0) | 2022.02.16 |
| ARIMAX를 이용하여 미국시장 전망 예측 <작성중> (0) | 2021.08.11 |
| 4가지 온라인 매체를 이용하여 유가 예측하기 (0) | 2021.08.06 |




댓글