출저: Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks (arxiv.org)
Github: GitHub - laiguokun/LSTNet
GitHub - laiguokun/LSTNet
Contribute to laiguokun/LSTNet development by creating an account on GitHub.
github.com
1. 개요
- 다중진동 시계열 분석은 실생활에서 흔히 볼 수 있는 현상 중 하나이다. 예를들어, 에너지 사용량이나 교통체증 시간 예측등은 단순 반복적인 시계열 현상보다는 수요가 몰릴 때 더 크게 진동하는 시계열 모델이 될 것이다. 위 논문에서는 이를 해결하기 위해, 딥러닝 프레임워크를 사용하였다. 위 딥러닝 프레임워크 LSTNet에서는 Convolution Neural Network와 Recurrent Neural Network 를 사용하여 짧은 진동 주기의 패턴을 추출하고 긴 진동 패턴또한 찾아내는데 사용한다. LSTNet 을 이용하여 한 시계열 예측은 보통 단순 ARIMA, VAR, LSTM 등만을 이용한 것 보다 눈에 띄는 성능 향상을 확인 할 수 있었다.
2. 배경
- 시계열 예측에서 가장 흔하게 쓰이는 ARIMA 모델같은 경우, 차원이 높아질 경우 예측값이 부정확해지는 문제점이 있다. (여기서 높은 차원의 경우 진동주기가 많아지거나 불규칙해지는 것을 의미한다) 이러한, 고차원 모델의 경우 VAR 모델을 사용하여 예측을 하는 방법이 있는데, VAR 모델 또한 장기적으로 볼경우 오버피팅 되기 쉬운 문제점이 있다. 이러한 문제들과 비슷하게, SVR, Gaussian Processes 또한 일반화문제나, 높은 컴퓨팅파워 문제들로 인하여 예측 정확도를 높이기가 쉽지않다.
3. 모델 설명
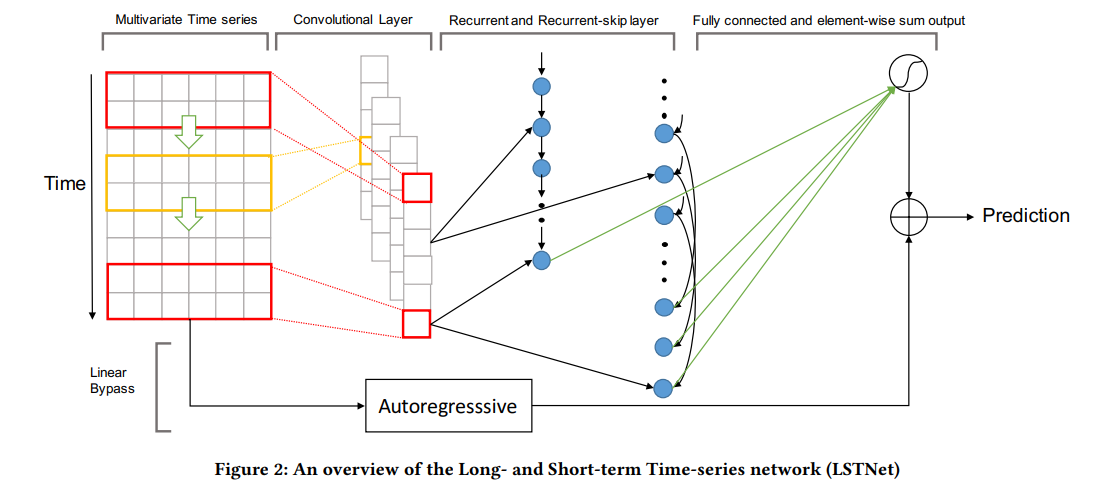
- 모델의 대략적 프레임워크는 위 Figure 2 와 같이 이루어진다.
먼저 첫번째 Layer 은 Pooling을 거치지 않은 Convolutional network로 시간 차원의 짧은 기간 패턴과 변수 간의 지역 의존성을 추출하는데 포커스를 두었다. Pooling 을 하지 않은 이유는 설명되어 있지 않지만, temporal dimension 을 만든것이지 실제 spatial dimension 을 다룬것 이 아니기 때문에 중요 정보를 잃지 않으려 Pooling 을 거치지 않은 것으로 보인다. Output matrix 는 input matrix X 와 weight matrix 의 convolution에 RELU를 적용하여 나온 값을 사용하며, Input 의 왼쪽 빈 값은 0으로 채워 넣는다 (zero-padding)
위 layer의 결과는 the Recurrent component 와 the Recurrent-skip component의 input 으로 사용된다.
Recurrent component는 GRU 모델과 ReLu를 사용하여 업데이트된 hidden function 이며 output 은 각 시계열별로 hidden state로 반환된다.
Recurrent Component

- ht: 시간 t 일 때의 은닉 상태
- xt: 시간 t일 때의 input
- rt: 리셋 게이트
- ut: 업데이트 게이트
- ct: 셀 상태
- Wxr, Whr, br, Wxu, Whu, bu, Wxc, Whc, bc: 각 게이트와 셀 상태에 대한 가중치 행렬과 편향
- ⊙: element-wise product
- σ: 시그모이드 함수
위 식은 각 time stamp 별 hidden state 를 계산하기 위한 식이다. reset gate와 update gate를 계산 후, Cell state를 계산한다 (ct) cell state 는 input에 가중치를 더한후 위에서 계산한 reset gate (rt)와 전 hidden state에 가중치를 더해 계산한다. 이렇게 새롭게 업데이트된 cell state에 먼저 계산된 업데이트 게이트를 사용하여 새로운 hidden state를 구한다.
Recurrent-skip Component
recurrent-skip component 는 GRU 와 LSTM 의 gradient vanishing 현상을 줄이고 더 정확한 예측을 하기 위해 사용된다. 위 컴포넌트는 실제 전기 소모량, 교통체증 과 같은 실제 시계열 데이터들을 더 정확하게 예측하도록 도와준다.

- xt is the input at time stamp t
- Wxr, Wxu, Wxc, Whr, Whu, Whc, br, bu, bc are learnable parameters of the network, representing the weights and biases of the input, recurrent and recurrent-skip components.
- σ is the sigmoid function, which is used to bound the output between 0 and 1
- rt = σ(xtWxr + ht−pWhr + br) is the update gate, which controls how much of the previous hidden state h_t-p should be passed to the current hidden state h_t
- ut = σ(xtWxu + ht−pWhu + bu) is the reset gate, which controls how much of the previous hidden state h_t-p should be forgotten in the current hidden state h_t
- ct = RELU(xtWxc + rt ⊙ (ht−pWhc ) + bc) is the cell state, which contains the information to be passed to the current hidden state h_t
- RELU(x) = max(0, x) is the rectified linear unit activation function, which is used to ensure non-negative values of the cell state.
- ht = (1 − ut ) ⊙ ht−p + ut ⊙ ct is the new hidden state, which is a combination of the previous hidden state h_t-p and the current cell state c_t. The combination is controlled by the update and reset gates
이전의 hidden state 와 (h_t-p) 현재 cell state (c_t) 를 이용하여 현재의 hidden state를 구하게 되며 업데이트 게이트와 리셋 게이트가 전으로 부터 얼만큼의 정보를 패스하고 잊어버릴지 정하게 된다. 여기서 중요한점은 p 인데, p 는 hidden state 를 업데이트 할때 얼마나 뒤의 정보를 봐야하는지를 결정하는 요소로, 뚜렷한 시계열 패턴이 있을경우 결정하기 쉽다 (예: p = 24 하루 시간별 변화를 관찰할 경우). 예를들어, 시간별 전기소모값을 나타낸 데이터를 사용한다면, p 는 24가 될 것이고, 이말은 recurrent-skip component가 전 24시간의 데이터부터의 hidden state 를 사용한다는 말이다. (하루중 9PM의 전기 소모량을 예측하기위해선, recurrent-skip component 는 전날 9PM 부터 오늘의 9PM까지 recurrent-skip component의 hidden state 를 사용한다.) 위를 공식으로 나타내면 아래와 같다.
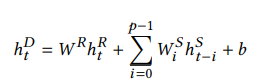
t 시간일때 hidden cell (h_t^R)과 hidden skip state의 24 -> 현재까지의 Sum을 더한 경우로 h_t^D (neural network 의 예측 결과)를 계산하게 된다.
Temporal Attention Layer
하지만 이러한 경우, p를 항상 사전에 알아야 한다는 문제점이 있다. 실제 시계열 데이터는 seasonal 하지 않으며 p를 찾을 수 없는 경우가 많은데 이를 보안하기위해 각 윈도우 마다 weighted combination 을 배우는 mechanism 을 적용하였다. 이러한 경우, 각 타임스탬프 마다 중요도를 비교하게되며, 가장 중요한 중요도를 계산에 적용시켜주게된다.
Autoregressive Component
Convolution 과 Recurrent 의 비선형적인 특성때문에 Neural Network는 input에 민감하지 않다는 단점이 있다. 실제 현실 시시각각 비규칙적으로 변하는 시계열 데이터는 이런 Neural Network를 썻을때의 한계를 넘지 못한다. 이를 보안하기 위해 위 논문에서는 비선형과 선형 파트를 나누는 방식으로 접근을 하였다. LSTNet은 시계열에서 많이 쓰이는 AR 모델을 선형데이터에 적용하였고, 비선형 데이터에는 convolution과 recurrent network 를 사용하여 학습을 하였다.
그리하여, 최종 예측값은 Neural network 파트랑 AR 파트를 더한 값을 두었다.

Data
LSTNet을 실험하기위해 사용된 퍼블릭 데이터들은 아래와 같다.
Traffic
Solar Energy
Electricity
Exchange-Rate
모든 데이터들은 60% 트레이닝 20% Validation 20% Test 셋으로 나눠 진행되었다.
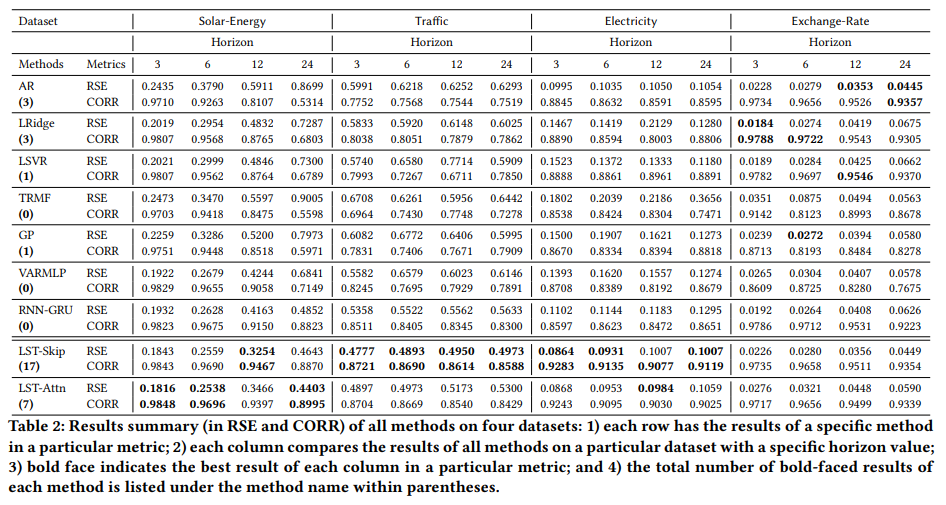
결과
'3. 심화 학습 (Advanced Topics) > 연구실' 카테고리의 다른 글
| 간단한 BERT 모델을 이용하여 GPT 챗봇 성능 높이기 (1) | 2023.11.23 |
|---|---|
| 시계열 분석에서 예측 모델의 구축 및 Stacking을 위한 베이지안 회귀 분석 방법 (2/2) - 구현 (0) | 2022.02.28 |
| 시계열 분석에서 예측 모델의 구축 및 Stacking을 위한 베이지안 회귀 분석 방법 (1/2) - 설명 (0) | 2022.02.16 |
| ARIMAX를 이용하여 미국시장 전망 예측 <작성중> (0) | 2021.08.11 |
| 4가지 온라인 매체를 이용하여 유가 예측하기 (0) | 2021.08.06 |




댓글